На этом шаге рассматривается оптимальное решение для двух игр с нулевой суммой.
Поскольку игра исходит из конфликта интересов, оптимальными решениями игры являются одна или несколько таких стратегий для каждого игрока, чтобы любое отклонение от этих стратегий не улучшало вознаграждение для одного или другого игрока. Эти решения могут быть в виде уникальных чистых стратегий или множества стратегий, смешанных в соответствии с предоставленными возможностями. Примеры, рассмотренные ниже, иллюстрируют описанную выше ситуацию.
Пример. Две компании A и B продают два разных лекарства от гриппа. Компания А рекламирует свою продукцию по радио (a 1), телевидению (b 2) и в газетах (a 3). Компания B рассылает листовки (b 4) в дополнение к использованию радио (b 1), телевидения (b 2) и газет (b 3). В зависимости от мощности и интенсивности рекламной кампании каждая компания может привлечь к себе клиентов своих конкурентов. Следующая таблица характеризует долю клиентов, привлеченных или потерянных фирмой.
Рисунок 1: Таблица характеристик
Решение игры основано на обеспечении наихудшего возможного исхода для каждого игрока. Если фирма A выбирает стратегию A 1, независимо от того, какая фирма B, наихудший исход заключается в том, что фирма теряет 3% рынка в пользу фирмы B. Это определяется минимальным значением элемента первой строки в таблице выплат. Аналогичным образом, если выбрана стратегия A 2, то наихудшим исходом для фирмы A будет рост на 5 % относительно фирмы B. Наконец, если выбрана стратегия A 3, то наихудшим исходом будет потеря фирмой A 9 % рынка в пользу фирмы B. Эти исходы включены в младший столбец строки. Чтобы достичь оптимального результата при наихудшем исходе, компания A выбирает стратегию A 2, поскольку она соответствует наибольшему элементу в столбце «минимальная линия».
Рассмотрим стратегию компании b. Поскольку в таблице указаны платежи компании, критерий «худший исход — лучший исход» для компании B соответствует варианту с минимаксной ценой. Следовательно, мы приходим к выводу, что выбором для фирмы B является стратегия B 2.
Наилучшим решением в игре является выбор стратегий 2 и B 2. Это означает, что обеим компаниям необходимо разместить рекламу на телевидении. В этом случае покупки увеличатся на 5 %, а значит, прибыль будет в пользу компании А. В этом случае цена игры составляет 5 %, и считается, что фирмы A и B используют стратегии, соответствующие точке сканирования.
Решение точки скорби гарантирует, что ни одной из компаний не имеет смысла пытаться выбрать другую стратегию. Действительно, если фирма B переходит к другой стратегии (B 1, B 3 или B 4), фирма A сохраняет свой выбор стратегии A 2, что приводит к большим рыночным потерям для B (6 или 8 на 100). По той же причине у фирмы A нет причин для использования другой стратегии. Например, если она реализует стратегию A 3, это произойдет потому, что фирма B может использовать стратегию B 3, чтобы увеличить свой рынок на 9 процентов. Если компания A применяет стратегию A, то вывод тот же.
Оптимальное решение игры, соответствующее точке горя, не обязательно должно характеризоваться чистой стратегией. Напротив, оптимальное решение может потребовать случайного смешения двух или более стратегий, как в следующем примере.
Пример. Два игрока A и B играют в игру, основанную на бросании валюты. Игроки одновременно выбирают, независимо друг от друга, корону (d) или букву (p). Если результаты двух бросков монет одинаковы (т.е. GG или RR), игрок A получает от игрока B $1. В противном случае игрок a платит игроку b один доллар.
В следующей таблице выплат для игрока A показаны значения минимального элемента строки и максимального элемента столбца, соответствующие стратегиям обоих игроков.
Максимальные цены (цены) игры равны $1 и $1 соответственно. Поскольку эти цены не равны друг другу, игра не имеет решения для чистых стратегий. В частности, если игрок A использует стратегию G, то игрок B выбирает стратегию B P и получает доллар от игрока A. Если игрок B выбирает стратегию B P, то игрок B получает доллар от игрока A. Если это произойдет, игрок А может изменить стратегию A P, чтобы изменить исход игры и получить доллары от игрока B. Постоянный соблазн для каждого игрока выбрать свою стратегию говорит о том, что решение на основе чистой стратегии неприемлемо. Вместо этого оба игрока должны использовать подходящую случайную комбинацию стратегий. В данном примере оптимальная цена игры лежит между максимальной и минимальной ценой этой игры.
Максимальное (нижнее) значение ≤ игровое значение ≤ минимаксное (верхнее) значение.
Таким образом, в данном случае цена игры должна находиться во вселенной [-1. 1], измеряемая в долларах.
В следующих шагах представлены некоторые из этих вопросов.
Как принять оптимальное решение
Оптимальное решение — это решение, которое, согласно некоторым критериям, является наиболее правильным в конкретной ситуации.
Суть оптимального решения заключается в выборе предпочтительного варианта из всех существующих. Мерой предпочтительности обычно служит показатель качества.
Особенностью оптимального решения является его экспертность, то есть то, что решение принимается в соответствии с определенными критериями. Оптимальное решение — это случай, когда есть параметры выбора. Наблюдается фактор, оптимальный вариант может быть таким, но становится оптимальным при влиянии другого фактора.
Изучение проблемы оптимального выбора относится к теории принятия решений. Это прикладная область исследований, объединяющая методы статистики, математики, психологии и менеджмента. Он занимается изучением закономерности выбора людей для достижения определенного результата. В теории принятия решений выделяют регулирование и описание. Первая занимается теоретическими аспектами рационального принятия решений. Вторая описывает практические аспекты принятия решений.
Практическое применение методов принятия оптимальных решений
В финансовой сфере часто возникают проблемы, требующие не только поиска решения, но и выбора наиболее выгодного варианта. Такие проблемы называются оптимизационными. Они имеют два аспекта
Оптимальные решения принимаются с помощью математических вычислительных инструментов. Существует несколько типов оптимизационных задач, для которых подбираются подходящие параметры решения. К ним относятся производственные, транспортные, инвестиционные задачи, задачи распределения, а также задачи о путешествующем продавце и задачи о ранце.
Производственные задачи возникают при планировании ресурсов и рентабельности бизнес-операций. Прибыль может быть максимизирована путем выбора типов продукции и оптимальных объемов ее производства. Транспортные задачи решают проблему эффективного и результативного перемещения ресурсов и готовой продукции между различными объектами экономики. Транспорт считается оптимальным, если он наиболее экономичен. Инвестиционные задачи используются на практике для определения оптимального объекта для инвестиций. Проблемы делегирования помогают выбрать наиболее подходящего исполнителя для выполнения конкретной задачи.
Лучшими методами решения являются линейное и нелинейное программирование. В первом случае используется линейная функция первой 2-й степени или полином из набора инструментов. Если задача носит ограничительный характер, то решение осуществляется с помощью нелинейного программирования.
Таким образом, принятие оптимальных решений является одним из инструментов минимизации неопределенности в финансовой системе.
Основные параметры поиска решения
Существует три способа поиска решения задачи. Во-первых, вручную перебирать параметры до тех пор, пока не будет найдено оптимальное соотношение. Во-вторых, составить уравнения с большим количеством незнакомых параметров. В-третьих, ввести данные в Excel и использовать «поиск решения». Последний способ самый быстрый и, если вы знаете, как пользоваться функцией, покажет вам самое точное решение.
Поэтому используйте «Поиск решения» Excel для решения задачи и начните с математической модели. Существует четыре типа данных: фиксированные, переменные ячейки, целевые функции и пределы. К поиску решений мы вернемся чуть позже, а пока давайте рассмотрим, что содержит каждый из этих типов.
Постоянная ячейка — это входная информация. Она включает в себя маржинальную прибыль, стоимость каждой перевозки и правила потребления запасов. В нашем случае — производительность труда рабочих, их зарплаты, правило 1000 товаров. Константы также отражают ограничения и условия математической модели. Например, только неотрицательные или целочисленные значения. Вставляйте константы в таблицу по номеру или основному типу (количество, среднеквадратичное значение).
Ячейки с переменными — это переменные, которые в итоге будут видны. На рабочем месте это распределение 1000 продуктов между рабочими с минимальными затратами. В разных случаях существуют переменные ячейки или диапазоны. При заполнении функции «Поиск решений» важно оставить пробел в ячейке — программа сама найдет цену.
Функция «Цель» — это результирующий показатель, из которого Excel выбирает лучший. Чтобы понять программу, вы определяете функцию как тип, элементы которого являются оптимальными. Этот тип отображается в отдельной ячейке. Показатель результата может быть максимальным или минимальным значением или конкретным числом.
Ограничения — это условия, которые необходимо учитывать при оптимизации функции, называемой объективной функцией. К ним относятся размер инвестиций, продолжительность реализации проекта и объем спроса со стороны клиентов. В нашем случае это количество дней и количество сотрудников.
Примеры использования поиска решений
Теперь перейдем к объяснению самой функции.
1) Чтобы активировать «Поиск решения», выполните следующие действия.
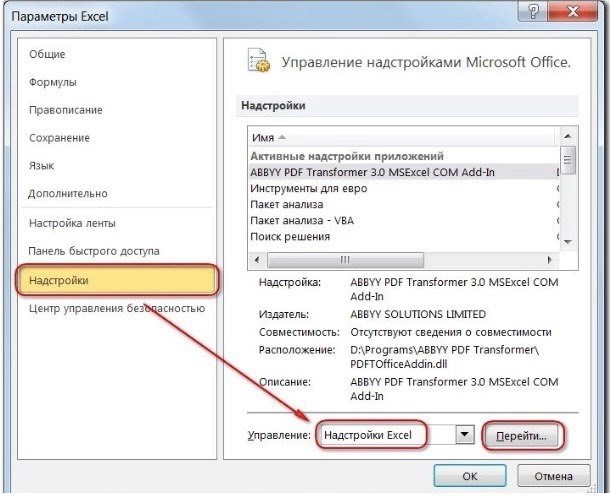
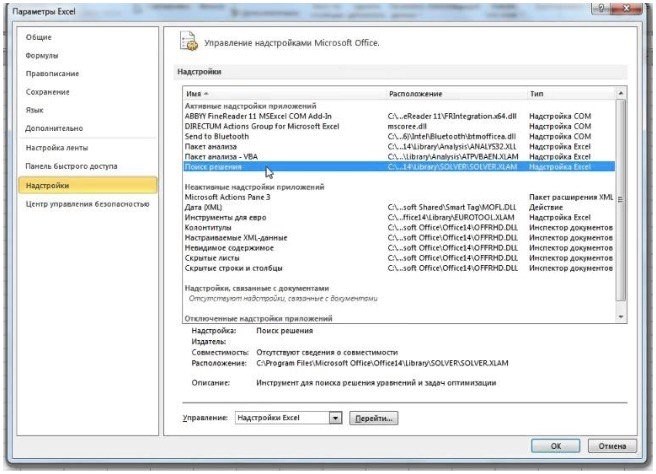
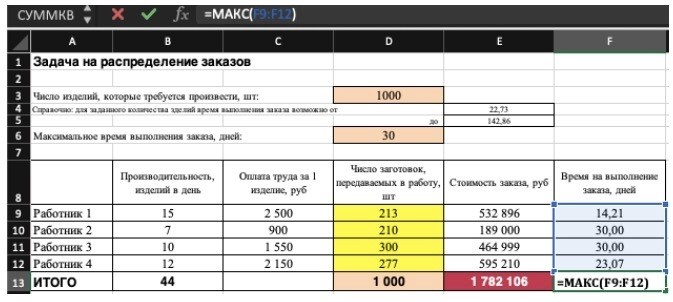
2) Далее организуйте данные в таблицу, показывающую взаимосвязи между ячейками. Рекомендуется использовать цветовое кодирование. В этом примере целевые функции выделены красным цветом, ограничения — бежевым, а ячейки, которые необходимо изменить, — желтым.
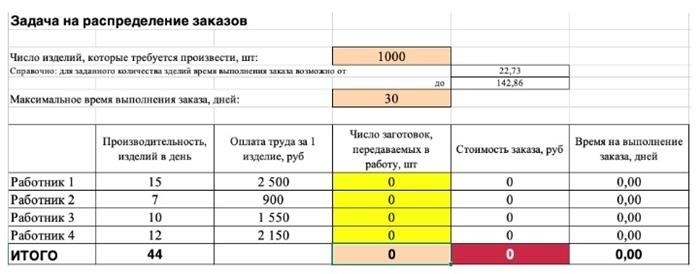
Не забудьте ввести формулу. Стоимость заказа рассчитывается как «стоимость работы за единицу» x «количество единиц для выполнения». Чтобы найти «время выполнения заказа», разделите «количество выполняемых заготовок» на «скорость производства».
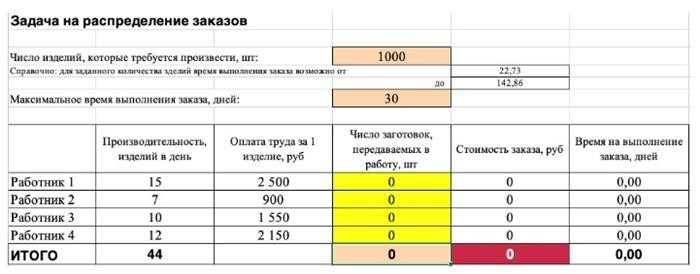
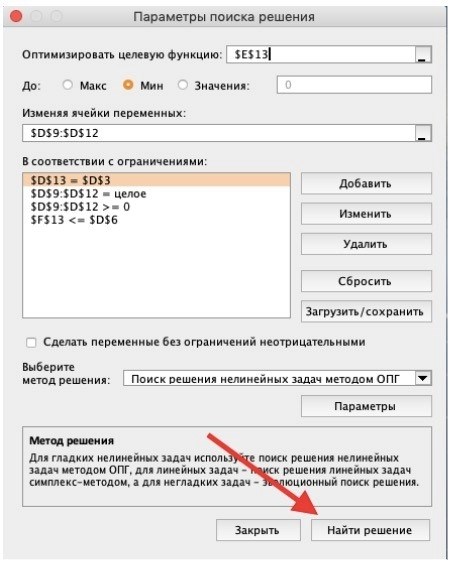
3) Выберите целевую ячейку для отображения максимального, минимального или определенного значения при заданных условиях. Для этого щелкните по опции «Данные» в таблице и выберите функцию «Найти решения» (обычно в правом верхнем углу).
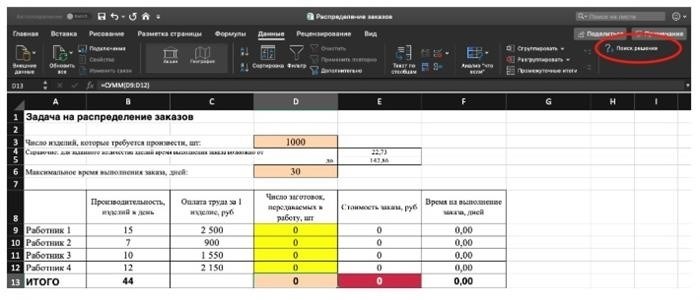
4) Введите параметры «Поиск решений» и нажмите кнопку «Поиск решений».
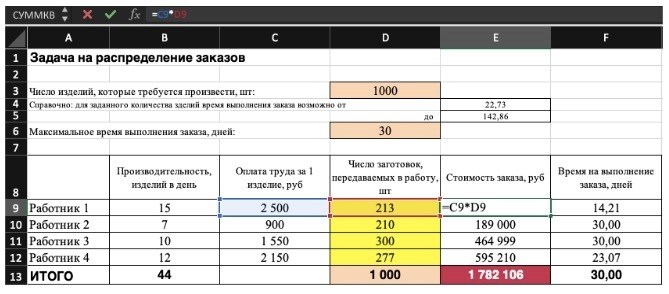
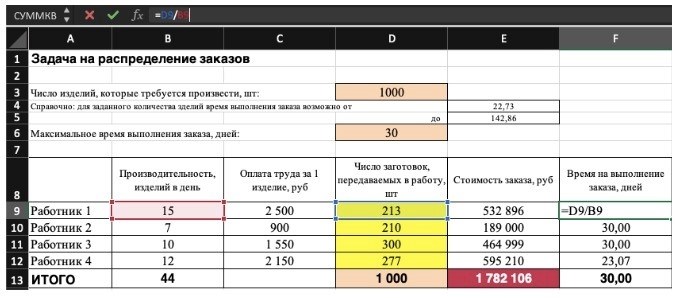
Совокупная стоимость 1 000 изделий рассчитывается как сумма затрат на количество изделий для каждого работника. Эта ячейка (E13) является целевой функцией. D9:D12 — переменные ячейки. В ходе «поиска решения» определяется оптимальное значение, при котором целевая функция достигает своего минимального значения при заданных ограничениях.
В данном примере используются следующие ограничения.
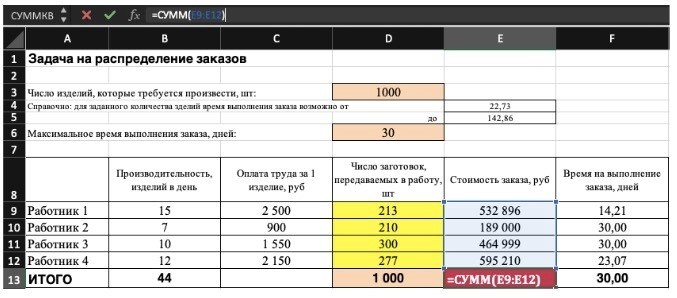
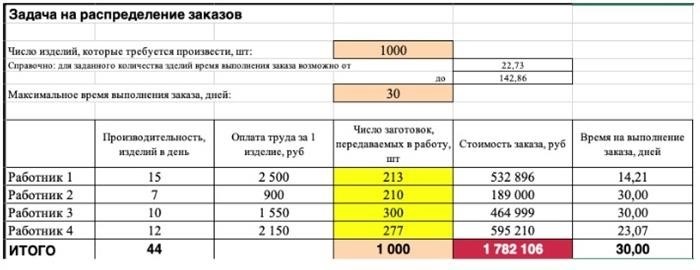
5) Наконец, проверьте, соответствуют ли полученные данные заданным целевым значениям. Если что-то не соответствует, необходимо исправить исходные данные, импортированные типы и ограничения.
Хотите знать, как решать задачи в Excel, как это делают ведущие компании? Получите доступ к онлайн-урокам, чтобы покорить этот инструмент на профессиональном уровне. Вас будут учить эксперты-профессионалы, и после обучения вы сможете добавить уверенную строчку в свое резюме. Записывайтесь!
Ярлыки.
Подпишитесь на информационные бюллетени о карьере
Подпишитесь на нашу рассылку и получайте советы по карьерному росту — от выбора отрасли и компании до лайфхакинга и навыков общения и самоменеджмента.